DES的差分分析攻击

差分密码分析介绍

差分密码分析是已知的攻击迭代密码（迭代一个简单的轮函数，比如DES，就是简单地根据F函数和密钥迭代N轮）最有效的方法之一，基本思想就是用过明文对的异或值对密文对的异或值的影响来还原密钥（也就是已知多对明文和密文，从而推测出密钥）。

一轮DES的差分密码分析

接下来用一轮的DES简单地演示一遍差分分析，附带python脚本

DES的密文是通过上一轮的R（32位），经过E-盒的扩充得到的E（48位），然后E与密钥经过PC-2置换的K（48位）异或后得到I，I经过分割后进入S盒，最终得到O，O经过P-盒置换得到P。（为了推理的简洁，之后的推论过程直接忽略E-盒置换和P-盒置换，因为这两个置换在差分分析的代码中加个逆置换就好了，所以下文中的E就是明文的右半部分，O就是密文的左半边部分）
从而得到以下公式
E⊕K=I
S（I）=O
之后我们还需要三个公式：
E’=（E） ⊕ (E#)
(E⊕K)⊕（E#⊕K）=（E⊕E#）（K⊕K）=E’
(E⊕K)⊕（E#⊕K）=I⊕I#=I’=E’

其中E和E#就是随机的一对明文，E’就是两者的异或值，同理可以得到I’、O’，在知道一对明文和轮函数（也就是DES的详细加密过程）的情况下，我们就能得到一对密文，从而得到E’、O’，因为K在不同明文的加密过程中是相同的，所以E’=I’，在知道I’、O’的情况下，我们也就能根据S-盒差分对应表得到可能的两个输入I、I#、接着通过已知的E、E#和多个可能的I、I#异或得到可能的K值，最后通过多对明文得到多个K值得集合，它们的唯一交集就是真正的K。

这里的难点在于O’通过S盒逆查找得到I’是有多种情况的，因为S盒是6位输入变成4位输出，这就造成了缺失，所以我们需要一个差分对应表，差分对应表的详情可以参考我的python代码
https://github.com/starsdestinations/DES-differential-cryptanalysis/blob/master/S%E7%9B%92%E5%B7%AE%E5%88%86%E5%80%BC%E5%AF%B9%E5%BA%94%E8%A1%A8python%E5%AE%9E%E7%8E%B0

我们可以得到一个I’（input）与O’（output）的差分对应表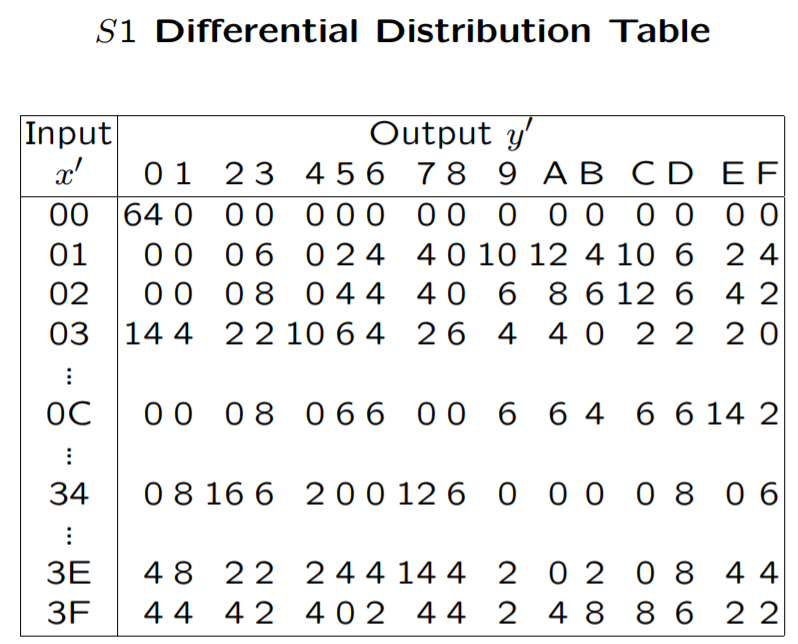

顺便一提的是一对输入I和I#顺序对调后得到的I’是一样的，所以差分对应表中每个项的值都是偶数

下面进行一次演示，只针对S1盒，所以我们选择两个6位明文
假设明文为E=0x13（01 0011） 和E#=0x27（10 0111）
得到E’=E ⊕ E# =0x13 ⊕ 0x27=0x34=I’
对两个明文进行加密（在不知道密钥的情况下，直接把两个明文放入黑盒DES中加密），得到两个密文，两个密文的O’值为D
根据I’ O’查找差分对应表，得到有4对（8种）可能的I值，经过计算得到这六个值为0x06、0x10、0x16、0x1c、0x22、0x24、0x28、0x32
把两个明文E和E#分别与这八个可能的I值异或：
0x06⊕0x01=0x07 0x06⊕0x35=0x33
0x10⊕0x01=0x11 0x10⊕0x35=0x25
0x16⊕0x01=0x17 0x16⊕0x35=0x23
0x1c⊕0x01=0x1d 0x1c⊕0x35=0x29
0x22⊕0x01=0x23 0x22⊕0x35=0x17
0x24⊕0x01=0x25 0x24⊕0x35=0x11
0x28⊕0x01=0x29 0x28⊕0x35=0x1d
0x32⊕0x01=0x33 0x32⊕0x35=0x07
将得到的16种可能的K作为一个集合{07，11，17，1d，23，25，29，33}

接着再选择一对明文，比如21、15，同样的顺序得到可能的K合集{00，14，17，20，23，34}
两个集合的交集{17，23}就是K可能取的值

通过多个明文对一次次的差分分析，最后我们会得到只有一个参数的交集，那个唯一参数就是K值